目次
はじめに:数学が苦手でもゲームは作れる
「ベクトル」という言葉を聞いただけで、高校時代の数学の記憶が蘇る方もいるのではないでしょうか。
ゲーム開発で使うベクトルは、数学の授業で習ったものよりずっとシンプルです。この記事では、数式をできるだけ使わず、「なんとなくわかる」を目指して解説していきます。
ベクトルって結局なに?
一言でいうと「矢印」です
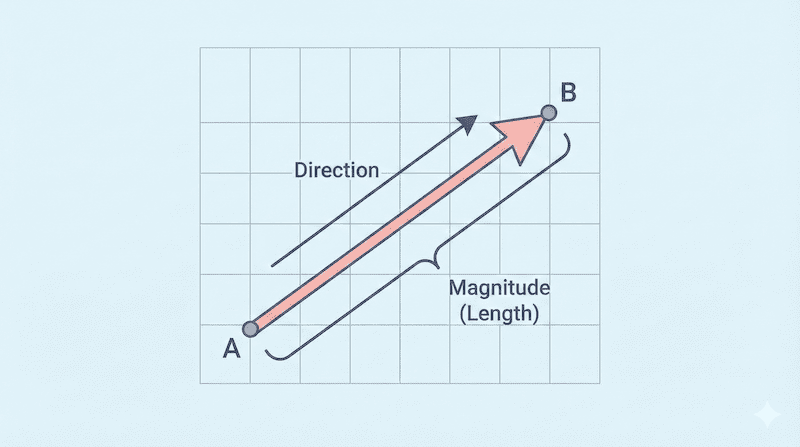
ベクトルを難しく考える必要はありません。「どの方向に、どれくらい進むか」を表す矢印、というイメージです。
たとえば、こんな指示を想像してください。
「北に向かって3メートル歩いて」
これがベクトルです。方向(北) と 大きさ(3メートル) の2つの情報を持っています。
ゲームでの具体例
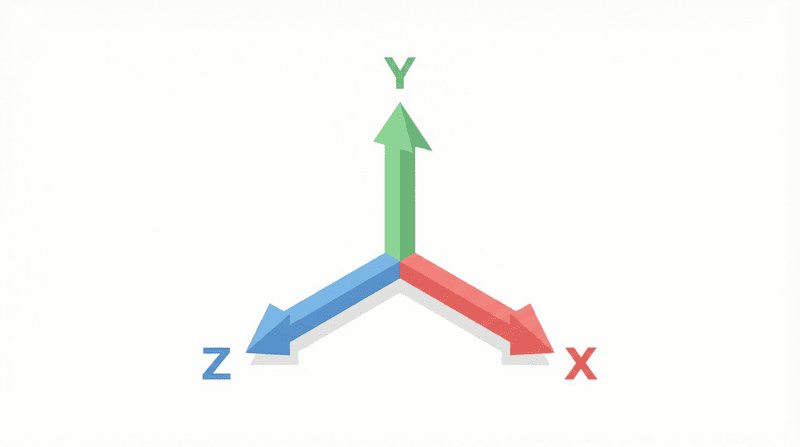
ゲーム開発では、Vector3という形でベクトルを扱います。これは3つの数字の組み合わせです。
Vector3(1, 0, 0) → X方向(右)に1進む
Vector3(0, 1, 0) → Y方向(上)に1進む
Vector3(0, 0, 1) → Z方向(奥)に1進む「え、3つも数字があるの?」 と思うかもしれませんが、単に「右に何歩、上に何歩、奥に何歩」を表しているだけです。
敵がプレイヤーを追いかける仕組み
ここからが本番です。ベクトルを使って「敵がプレイヤーを追尾する」処理を作ってみましょう。
ステップ1:方向を求める
敵からプレイヤーへの方向は、「目的地 − 現在地」 で求められます。
追いかける方向 = プレイヤーの位置 − 敵の位置
計算すると (5-2, 3-1) = (3, 2) という矢印が得られます。これが「敵からプレイヤーへ向かう方向」です。
ステップ2:正規化(Normalize)する
ここで問題が発生します。
プレイヤーが近くにいると矢印が短く、遠くにいると矢印が長くなってしまいます。このまま移動に使うと、遠い敵ほど速く動いてしまうことに。
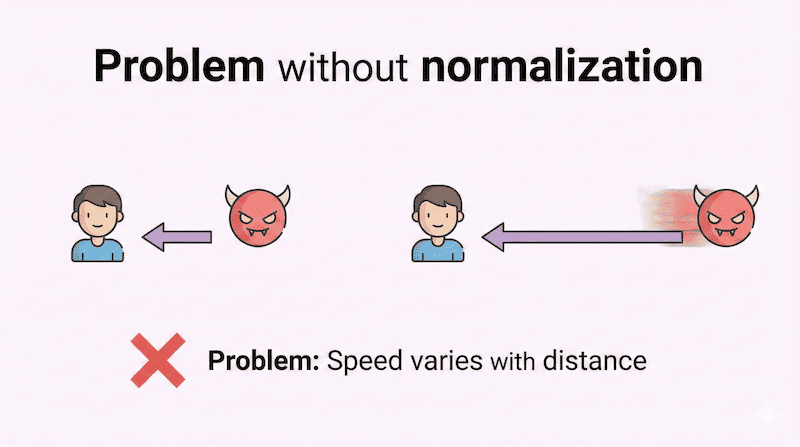
そこで登場するのが正規化(Normalize)です。
正規化とは?
矢印の長さを「1」に揃える処理です。方向はそのまま、長さだけを調整します。
正規化前:(3, 2) → 長さがバラバラ
正規化後:(0.83, 0.55) → 長さが1に統一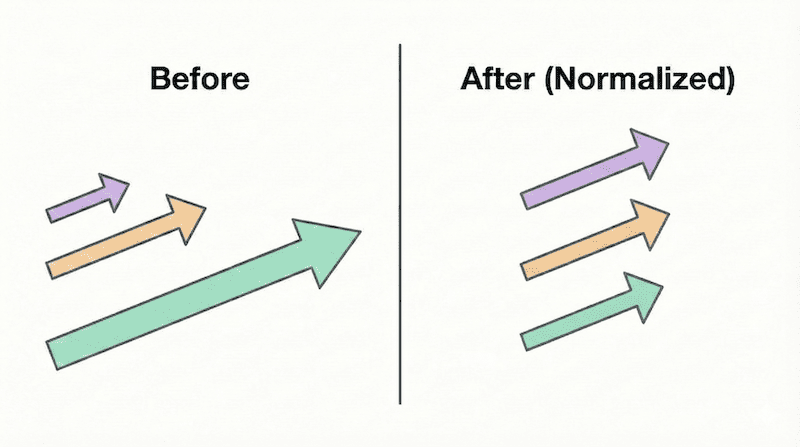
これで距離に関係なく、常に同じ速度で追いかけることができます。
ステップ3:速度をかける
最後に、正規化したベクトルに「移動速度」をかけて完成です。
// Unityでの実装例(敵自身のスクリプトに書く場合)
Vector3 direction = (player.position - transform.position).normalized;
transform.position += direction * speed * Time.deltaTime;たった2行で追尾AIの完成です!
弾をまっすぐ飛ばす
弾の移動も同じ考え方です。
private Vector3 shootDirection;
void Start() {
// 【発射時】生成された瞬間に1回だけ計算!
shootDirection = (target.position - transform.position).normalized;
}
void Update() {
// 【毎フレーム】決まった方向に飛び続ける
transform.position += shootDirection * bulletSpeed * Time.deltaTime;
}ポイントは、発射時に方向を決めて保存しておくこと。毎フレーム方向を計算し直すと、弾が追尾ミサイルになってしまいます(逆に言えば、これがホーミング弾のロジックです)。
距離の計算
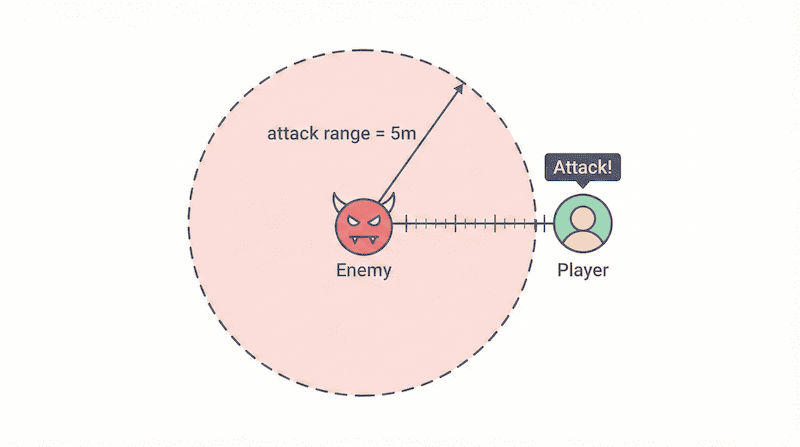
「プレイヤーが近づいたら攻撃する」といった処理には、距離の計算が必要です。
便利メソッドを使おう
UnityならVector3.Distanceを使うだけでOKです。
float distance = Vector3.Distance(enemy.position, player.position);
if (distance < 5f)
{
// 攻撃開始!
}中身の計算(三平方の定理)を知らなくても、まったく問題ありません。
パフォーマンスTips
距離の比較だけなら、sqrMagnitudeを使うと少し高速です。
// 5メートル以内かどうかを判定
if ((player.position - enemy.position).sqrMagnitude < 25f) // 5の2乗
{
// 攻撃開始!
}大量の敵がいるゲームでは、このちょっとした工夫が効いてきます。
よく使うベクトル操作まとめ
| やりたいこと | コード |
|---|---|
| AからBへの方向 | (B - A).normalized |
| 2点間の距離 | Vector3.Distance(A, B) |
| ベクトルの長さ | vector.magnitude |
| 長さを1にする | vector.normalized |
| 2つのベクトルを混ぜる | Vector3.Lerp(A, B, 0.5f) |
まとめ:ベクトルは「矢印」と覚えよう
- ベクトル = 方向と大きさを持つ矢印
- 方向を求める = 目的地 − 現在地
- 正規化 = 長さを1に揃えて、速度を扱いやすくする
- 距離 =
Vector3.Distanceに任せる
数学的な理解は後からついてきます。まずは「こう書けば動く」を体験して、ゲーム作りを楽しんでください!




